Insegnare con la calcolatrice grafica
In questo testo si vuole indagare la relazione che sussiste tra la media aritmetica e geometrica di due numeri. Tutto ciò avverrà attraverso un dialogo tra una studentessa di 16 anni, la protagonista, e Memole, impersonificazione della sua calcolatrice grafica. I due personaggi possono inoltre contare sull’ausilio di un’intelligenza artificiale, alla quale possono far ricorso ogni qual volta si voglia aver una conferma sulle proprie congetture o si abbia bisogno di qualche indizio.
(In questo dialogo utilizzeremo la calcolatrice grafica Casio FX-CG50)
Dialoghi con la calcolatrice
Media aritmetica e media geometrica
Cami: Ciao Memole!
Memole: …
Cami: Ops, che sciocca, mi son dimenticata di accenderti! Rimedio subito con il tasto AC/ON.
Memole: Ciao!
Cami: Finalmente eccoti! Abbiamo un nuovo compito per oggi. Per favore, mi potresti dare due numeri casuali?
Memole: Certamente! Ma perché io sia in grado di farlo, utilizza un mio comando.
Cami: Hai ragione! Allora… Come si faceva… Innanzitutto, apriamo uno dei Menu. Proviamo dal primo, il Menu RUN-MATRIX. Vediamo un po’ che comandi ci sono… JUMP, DELETE; MAT/VCT, MATH… Clicco F4, proviamo con MATH… Non mi sembra ci siano comandi utili in fondo alla riga, mi sembra che si dovesse usare un altro tasto… Ma che altre opzioni ci sono? Ma che sciocca, come dice la parola stessa, proprio il tasto Option OPTN! Era così semplice… Dopodiché, F6 per scorrere la pagina e F3 per selezionare PROB… Ed ora F4 per utilizzare il comando RAND!
Memole: E poi?
Cami: Ancora F1 e finalmente seleziono Ran# e premo Enter per farti eseguire il comando.
Memole: Ecco il tuo numero: 0,7187…
Cami: Me ne hai dato uno… ora ne vorrei un altro!
Memole: Premi di nuovo lo stesso comando!
Cami: F1… Ran# e poi enter…
Memole: 0,1134…
Cami: Proviamo ancora…

Leggi ancora – Parte 2, spreadsheet:
Cami: Noto qualcosa di strano… Mi sembra che tutti i numeri casuali sono minori di 1? Anzi, sembrano essere anche sempre positivi. Ho ragione Memole?
Memole: Sì, è proprio così! Il mio libretto di istruzioni me lo ha appena confermato!
Cami: Come posso dunque ottenere un numero casuale maggiore di 1? Qualche modo dovrà pure esserci, ma non mi viene proprio in mente nulla. Proviamo a chiedere un indizio…
Memole: Sì, chiediamo ad AI!
Cami: Ciao AI! È possibile ottenere, con l’aiuto di Memole, un numero casuale più grande di 1?
AI: Sì!
Cami: E come?
AI: Non ti darò la soluzione, ma solo un indizio. Usa una combinazione di uno o più tasti di Memole.
Cami: Mmh… Fammici pensare… A partire da un numero compreso tra 0 e 1, voglio ottenerne uno sicuramente più grande di uno… Potrei aggiungere 1 al risultato oppure… oppure che idea moltiplicare per 10, ad esempio! Memole mi calcoleresti un po’ di numeri 10*Ran#? Memole: Ecco a te! 8,88… 7,54… 0,93… 5,42…
Cami: Fantastico! Vediamo un po’ che altre proprietà possono avere questi numeri ”casuali”. Ad esempio, se faccio il prodotto Ran#*Ran#, cosa succederà?
Memole: Ran# × Ran# = 0,2853…
Cami: Okay, però così non ho informazioni, mi sono persa i numeri casuali di partenza! Riproviamo…
Memole: Ran#=0,6197…, Ran#=0,0382…
Cami: Calcolami il loro prodotto!
Memole: Mi sono dimenticata i numeri…
Cami: Ti dimentichi sempre tutto, sempre la stessa storia! Come faccio a fartele ricordare?
Memole: Non è colpa mia! Potresti utilizzare la mia memoria!
Cami: Ma che memoria hai se non ti ricordi niente?
Memole: Devi riempire tu la mia memoria…
Cami: Ma come posso fare… Fammici pensare… Ah ecco! Potrei assegnare i tuoi valori a delle variabili, così non te li scorderai più!
Memole: Hai ragione, ma quanto sei brava! Così ogni volta che ne avremo bisogno potrò richiamarle alla mia ”memoria”.
Cami: Allora… Assegna il primo Ran# alla variabile A… e il secondo alla variabile B…
Memole: Ran# = 0, 6197… → A, Ran# = 0, 0382… → B
Cami: Memole, ora mi faresti questa operazione? A × B?
Memole: Ta daaaan: A × B = 0, 0236
Cami: Fantastico!
Memole: Inoltre io ho anche altre funzioni che possono velocizzare il tutto! Prova a controllare anche gli altri Menù…
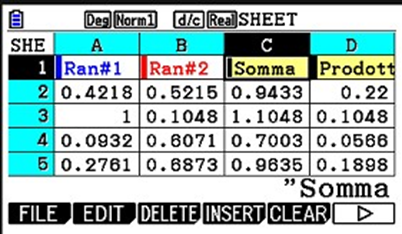
Cami: Potremmo creare un foglio di calcolo con il Menù SPREADSHEET! Nelle colonne A e B inserisco i numeri ”casuali” generati con il comando Ran#, mentre nelle colonne C e D creo delle funzioni: la colonna C conterrà le somme dei numeri nella medesima riga di A e B, mentre la colonna D il prodotto di tali numeri.
Memole: Ottima idea! In questo modo potremmo visualizzare tutte le informazioni contemporaneamente e ci sarà più facile giungere ad una congettura! Ecco il tuo foglio di calcolo:
Istruzioni dettagliate per la costruzione di un foglio di calcolo:
Selezionare il Menù SPREADSHEET. Per inserire le stringhe di testo è necessario anteporre delle virgolette (”) alla stringa. Per la creazione di funzioni si opera nel seguente modo: selezionare la cella interessata, nel nostro caso la cella C2, dopodiché F2 per selezionare EDIT, F6 ed F1 per selezionare il comando FILL. Inserire ora la formula che interessata, nel nostro esempio inseriremo =A2xB2 e come Cell range impostare, sempre nel nostro caso, C2:C5. Premiamo EXE. Poiché abbiamo fatto precedere la formula da un uguale, la formula verrà estesa a tutte le celle che abbiamo selezionato nel Cell range. Poiché abbiamo inserito l’uguale davanti alla formula, l’indice di riga viene aggiornato automaticamente, quindi, nella cella C3 otterremo =A3xB3 e così via… abbiamo così creato un riferimento dinamico; se invece non avessimo inserito l’uguale, avremmo creato un riferimento statico e avremmo ottenuto il risultato dell’operazione A2xB2 in tutte le celle.
Leggi ancora – Parte 3, nuova colonna “media aritmetica”:
Cami: Ora riusciamo a vedere chiaramente tutto! Noto ancora una volta che i numeri ”casuali” sono tutti compresi tra 0 e 1, in più ho anche delle osservazioni riguardo la somma e il prodotto di tali numeri: la somma è sempre più grande dei suoi addendi, essendo essi sempre positivi, perciò anch’essa è sempre positiva; inoltre noto dalla seconda riga che può essere anche maggiore di 1, perciò può anche non appartenere all’intervallo [0,1]. Il prodotto invece è sempre minore dei valori iniziali ed è sempre positivo, entrambe queste due osservazioni mi portano dunque ad affermare che il prodotto appartiene sempre all’intervallo di partenza [0,1].
Memole: Fantastico, sei proprio brava! Che altro osservi?
Cami: Ora… ho trovato delle funzioni (somma e prodotto), dipendenti dai miei valori iniziali, che mi restituiscono sicuramente valori più grandi e più piccoli (rispettivamente) dei miei dati casuali di partenza.
Memole: Beh raccontiamolo ad AI. Vediamo cosa ci dice.
Cami: AI, come dicevo, abbiamo scoperto che la somma e il prodotto di due numeri casuali, compresi tra 0 e 1, sono rispettivamente più grandi e più piccoli dei miei numeri di partenza.
AI : Ma sei capace di visualizzarlo?
Cami: Visualizzarlo?
AI : Sì, ho detto proprio questo.
Cami: Ho capito, come al solito non mi dirai nulla di più… Beh per visualizzare qualcosa forse dovrei crearmi un’immagine ”mentale”, giusto?
AI : Sì.
Cami: Beh, potrei considerare i miei numeri ”casuali” come estremi di un intervallo… la loro somma e il loro prodotto non appartengono dunque a questo intervallo. AI, ma tu sai anche cos’è che potrebbe sicuramente essere contenuto al suo interno?
AI : Io? Che domande, ovvio che lo so! E tu?
Cami: Fammici pensare… Qualcosa sicuramente all’interno di un intervallo… Ma certo, la sua metà! Quindi, se chiamo a il primo numero e b il secondo, il ”punto medio” dell’intervallo – che sarà sicuramente contenuto – sarà $\dfrac{a + b}{2}$ .
AI: Ti è nuova questa forma?
Cami: In effetti questa forma mi ricorda qualcosa… Ah si, la media aritmetica!
Memole: Perché non mettiamo anche la media nel foglio di calcolo!
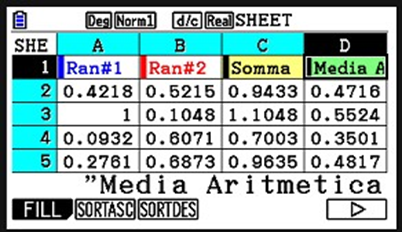
Cami: Hai ragione! Costruiamo una nuova colonna e la chiamiamo ”Media Aritmetica”. Come prima inseriamo la funzione…
Memole: Quale?
Cami: =A+B/2… Ma come mai non vedo nulla? Ah si, ci siamo scordati di premere invio!
Memole: Ecco a te!
Leggi ancora – Parte 4, nuova colonna “media geometrica”:
Cami: Ciò che abbiamo fatto alla fine è stato prendere la somma di due numeri, che era più grande di entrambi, e riportarla nell’intervallo dividendola per due… Sarà possibile far qualcosa del genere anche con il prodotto, che è invece sempre più piccolo?
Memole: Mi sembra una bella domanda da porre ad AI…
AI: Sì, esiste un altro tipo di media, detta media geometrica, che tra due numeri e calcolata come la radice quadrata del prodotto dei due.
Memole: Facciamo una colonna anche per questa!
Cami: Va bene Memole!
Memole: Ecco qui:
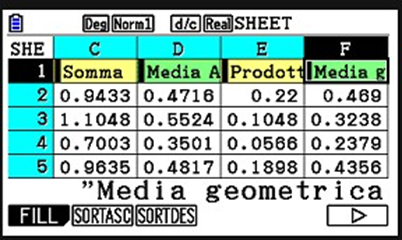
Leggi ancora – Parte 5, dimostrazione geometrica:
Cami: Wow! Funziona!
Memole: Allora ricapitolando: ”Dati due numeri qualsiasi a e b prodotti da Ran#, la radice quadrata del loro prodotto ($\sqrt{ab}$) e la metà della loro somma $\dfrac{a + b}{2}$ sono sempre contenute nell’intervallo [a,b].”
Cami: Non pensavo che tutti i numeri compresi tra 0 e 1 avessero questa proprietà, è meraviglioso! AI, visto che scoperta?
AI : Pff, che ”scoperta”… L’umanità è a conoscenza di questa proprietà da secoli… Comunque, il tuo risultato è giusto, ma c’è di più, vale addirittura per tutti i numeri positivi! Altro che la tua di scoperta…
Cami: Come al tuo solito sei sempre cosı indisponente AI, pensi di sapere tutto!
AI : Ma io so tutto!
Cami: Vabbeh, lasciamo perdere… Ora però son curiosa… Quale delle due medie è più grande? Ovviamente entrambe sono interne all’intervallo [a,b], ma saranno diverse! Dalla tabella osservo che la media geometrica è più piccola di quella aritmetica.
Memole: Dunque: ”la media geometrica tra due numeri è sempre minore della media aritmetica tra gli stessi”.
Cami: Aspetta un attimo Memole… Ma questo è sempre vero? AI, cosa ne pensi?
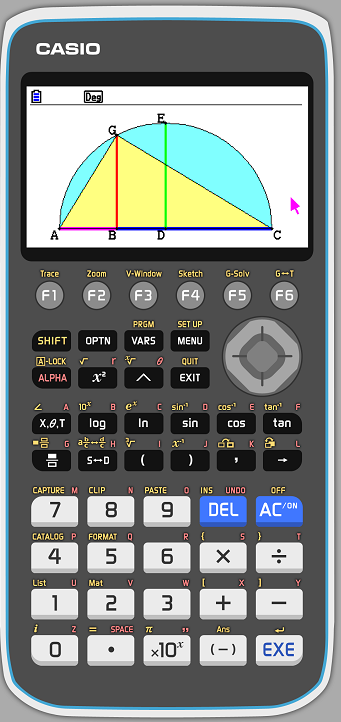
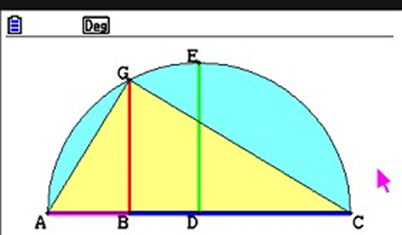
AI : Sì, è vero, ma ricordati che la media geometrica esiste solo tra numeri positivi! Eccoti una piccola dimostrazione della vostra congettura. Prima però, con l’ausilio di Memole, fai questa costruzione geometrica: costruisci due segmenti, AB e BC. Le lunghezze di questi due segmenti rappresenteranno i tuoi numeri di partenza. Fa’ in modo che i tre punti A, B e C siano allineati. Sia D il punto medio di AC e costruisci la perpendicolare ad AC passante per D. Essa incontrerà la semicirconferenza nel punto E. Ora, costruisci la semicirconferenza di diametro AC e la perpendicolare ad AC passante per B, chiamiamola s. Interseca s con la semicirconferenza, ottenendo così il punto G. Costruisci ora il triangolo ACG: questo triangolo e inscritto in una circonferenza e insiste su un diametro, dunque è un triangolo rettangolo.
Memole: Ho eseguito tutti i comandi, ecco qui quel che ottengo:
Istruzioni dettagliate per la costruzione della figura:
Selezionare il Menù GEOMETRY. Creare un nuovo File con premendo F1 e selezionare New con [1]. Premere invio. Per disegnare i segmenti premere F3 e Line Segment [2]. Spostare il cursore nel punto in cui si vuole creare il primo estremo del segmento, premere EXE e poi spostare nuovamente il cursore sino al punto che vogliamo identificare come secondo estremo. Premere di nuovo EXE, il segmento è così creato. Procedere allo stesso modo per costruire il secondo segmento. Per costruire la semicirconferenza, premere F3 e SemiCirc [8], selezionare il diametro su cui vogliamo costruire la semicirconferenza (è sufficiente selezionare gli estremi del diametro) e premere EXE. Per trovare il punto medio di un segmento, è necessario selezionarlo (cliccandoci sopra) e premere F4, Midpoint [3]. Per costruire una perpendicolare ad una data retta (o segmento) in un determinato punto è necessario selezionare quest’ultimi, cliccandoci sopra, e utilizzare il comando F4, Perpendicular [2]. Infine, per ottenere dei punti come intersezione di rette, segmenti o semicirconferenze, è necessario selezionare le figure interessate e utilizzare il comando F4, Intersection [4]. È possibile personalizzare le figure, cambiando ad esempio colore e spessore delle righe o il riempimento delle stesse, selezionando l’oggetto interessato e utilizzando il comando OPTN.
Leggi ancora – Parte 6, formule ricorsive:
AI : Ora… La media aritmetica è rappresentata dal raggio della semicirconferenza, nel nostro caso il segmento ED. La media geometrica è rappresentata invece dal segmento GB. Come puoi notare GB, qualsiasi siano le misure di partenza di AB e BC, sarà sempre più piccolo di ED. L’unica eccezione è quando AB e BC sono di egual misura: in quel caso le due medie saranno uguali.
Cami: Interessante, quella aritmetica è sempre più grande… Ma come mai GB rappresenta la media geometrica?
AI : Per il teorema di Euclide, ovviamente! AGC è un triangolo rettangolo in G e GB è l’altezza relativa alla base AC. Dunque $GB^2 = AB \times BC$. Da questo, possiamo ricavare: $GB = \sqrt{ AB \times BC}$
Cami: Chiaro! Assomiglia proprio all’espressione della media geometrica.
AI : Ma certo, non solo ci somiglia, è proprio quella!
Cami: Ma ora sono curiosa… Ogni volta posso restringere il mio intervallo iniziale, prendendo come estremi la mia media geometrica e quella aritmetica. Il mio nuovo intervallo potrà mai diventare così piccolo da essere solamente un punto, cioè i due estremi coincideranno mai?
Memole: Credo di avere una funzione anche per questo…
Cami: Fammi controllare i vari Menu… RUN-MATRIX no, GRAPH potrebbe… ma vediamo prima cos’altro c’è… RECURSION, interessante… e se usassimo delle formule ricorsive? Che dici Memole?
Memole: Che grande idea! Sai io sono anche in grado di mostrarti una schermata grafica!
Cami: Okay, proviamo allora! Apro il Menu RECURSION. Per prima cosa imposto i valori iniziali e scrivo le formule ricorsive… Ma come si fa?
Memole: Cosa vuoi fare di preciso?
Cami: Ad ogni passo, vorrei che la media geometrica diventasse l’estremo inferiore dell’intervallo, mentre la media aritmetica l’estremo superiore… E così via. In questo modo l’intervallo si dovrebbe stringere ad ogni passo!
Memole: Bravissima, ci sei! Prova a trasformare in formule questo pensiero, così posso digerirle pure io!
Cami: Allora… Facciamo due formule ricorsive, una per la media aritmetica e una per la media geometrica… Devo solo esser brava a far incastrare le due! Quindi, voglio una formula che al ”passo successivo” utilizzi i valori trovati nel ”passo precedente”.
Memole: Nel mio libretto di istruzioni parlano di indici… Strano, noi calcolatrici non abbiamo le mani!
Cami: Memole, sei un genio! Ovviamente le calcolatrici non hanno dita, gli indici vengono utilizzati per indicare il passo della formula al quale ci troviamo! Sono dei numerini che si mettono in basso, mi sembra di aver imparato questo oggi a scuola. Allora… Nel tuo Menu utilizza n… Ma che cos’è?
AI : Il passo generico, l’ennesimo! Scusatemi, ero rimasta accesa e non ho potuto far a meno di rimediare ai vostri sciocchi e umani errori!
Cami: Grazie AI! Quindi, se ne il passo generico, il passo successivo sarà n+1! Se ora denoto con $a$ le medie aritmetiche e $b$ quelle geometriche, con un po’ di lavoro, dovrei ottenere questo:
$a_n+1 = a_n + b_n$ e $b_{n+1} =\sqrt{a_n b_n}$
Memole: Ecco qui!

Leggi ancora – Parte 7, visualizzazione formule ricorsive:
Cami: Ops! Memole mi stavi quasi per cadere! Che sciocca ho premuto F5, cos’è questa schermata strana?
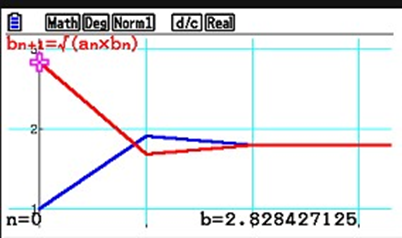
Memole: Ecco ciò di cui ti parlavo prima, il grafico dei valori! Hai selezionato GPH-CON, grafico continuo!
Cami: Io comunque questa schermata non la capisco molto…
Memole: Magari AI e capace di spiegarcela!
AI : Certo che ne son capace, avevate dubbi? Avete impostato il passo uguale ad 1, perciò dovete considerare solo i valori con ascissa intera. L’asse orizzontale rappresenta proprio il passo della formula ricorsiva, mentre quello verticale il valore effettivo che le medie assumono.
Cami: Allora… La linea azzurra rappresenta la media aritmetica, quella rossa quella geometrica. Da qui si vede molto bene che la nostra congettura di prima e vera! Ad ogni passo sono sempre più vicine, ma la relazione che intercorre tra le due non cambia. Inoltre sembra davvero che le due medie prima o poi si sovrappongano, significa che i valori prima o poi saranno uguali!
Istruzioni dettagliate per la costruzione delle formule ricorsive e il loro grafico:
Istruzioni dettagliate per la costruzione delle formule ricorsive e il loro grafico: Selezionare il Menu RECURSION. Utilizzare F3 per scegliere il tipo di formula ricorsiva, nel nostro caso sceglieremo la seconda (formule del tipo an+1=…), perciò premiamo F2. Inseriamo le nostre formule ricorsive, utilizzando, dove necessario, F4 per inserire caratteri speciali (come n, an, bn…). Premiamo SET [F5] per impostare i nostri parametri iniziali e il numero di iterazioni che vogliamo fare. Premendo TABLE [F6], è possibile visualizzare, in una tabella, i valori delle formule ricorsive ad ogni passo. Dalla schermata TABLE, premendo GPH-CON [F5] è possibile visualizzare il grafico connesso dei nostri punti, che avranno come ordinata il valore assunto dalle formule e in ascissa il passo. Nella schermata grafica, per una buona visualizzazione è molto importante scegliere lo zoom adatto: ciò sarà possibile utilizzando il comando F2.